How to Calculate the Taylor Series Approximation for the Sine Function

Taylor Expansion for the Sine Function upto the first five terms. All powers are odd as the sine function is odd.

The Taylor series approximation gives the value of the function based a finite number of terms from an infinite series. The infinite number of terms that add up to the function are obtained from the derivatives of the function at a single point. At x=0, these terms give the Maclaurin series for the function. Let us see how to calculate the value of the commonly used function sin(x) using Taylor Approximation.

• If we read the input in degrees, we first need to convert it to radians. In simple words, this is because the derivative of sin(x) is not simply cos(x), when x is in degrees. It is instead (π/180)cos(πx/180), where x is in degrees.
• Summing up the terms in using the value in radians is easy. We can perform similar calculations for cosine, logarithmic functions, etc.
• Finally, we compare the results with that obtained from the intrinsic function in FORTRAN just to make sure  the program executes correctly.

Now for the FORTRAN program,

!To find the sine value using Taylor expansion
program Taylor
    implicit none
    real x,t,angle,sum1,sum2
    integer np,n,i
   
    !To read the angle in degrees
    write (*,*) "Give the number whose sine value you wish to compute (in degrees)"
    read (*,*) x
    write(*,*) "Calculating the sine of ",x
   
    !To convert the angle to to radians
    angle=0.0174532925*x
    write (*,*) "The angle in Radians is= ",angle
    write (*,*) "Give the value of n (the no. of terms in the Taylor series)"
    read (*,*) n
    write (*,*) "The given value of n (the no. of terms in the Taylor series) is ",n

    !To sum up terms in Taylor series
    t=angle
    sum1=angle
    np=(2*(n-1))+1
    do i=3,np,2
        t=(((-t)*(angle**2))/(i*(i-1)))
        sum1=sum1+t
    end do
    write (*,*)  "By Taylor series, sin(",x,")= ",sum1

    !To compare value using the intrinsic function
    sum2=sin(angle)
    write(*,*) "By using the intrinsic function, sin(",x,")= ",sum2
    if ((abs(sum1-sum2))<0.00001) then
        write(*,*) "The result matches the value given by the intrinsic function"
        else
        write(*,*)"The value found does not match the value given by the intrinsic function"
    end if

end program Taylor
     

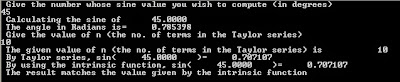Sample Output for the Taylor Approximation of the Sine Function