How to find the GCD of A Set of Numbers

To find the GCD of numbers using Euclid's algorithm is very easy. Let us discuss this algorithm first.

Simply put, when  we have two numbers x and y, the larger one(y1) is either divisible by the smaller one(x1) or it isn't (More often than not).

If y|x, then gcd (x, y) = x.

This is the simplest scenario.

Now, if we have a remainder (i.e. a non-zero modulus), we replace this as the next x1 value and use the previous x1 as y1( i.e. the new larger number). Now, we continue this process till we get a remainder of zero.

If y1 = x1.q + r, for integers q and r, then gcd (x1, y1) = gcd (x1, r)

 This way, we continue replacing values of y1 and x1, till we get the GCD.

The values of X and Y are updated till we get the remainder zero.

In the program, I have added a loop to find the GCD of more than two numbers. The GCD of three numbers is the GCD of  the GCD of the first two numbers and the third number. We continue taking the GCD of the GCD of the numbers included so far and the new number added till we have included all the numbers.

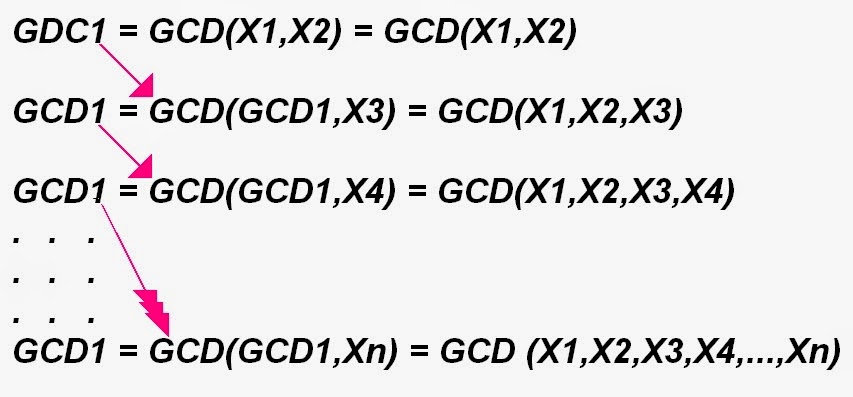Finding the GCD of a Set of Numbers

Now for the Fortran program,

 !To find the GCD of the given numbers
program gcd_all
    integer, allocatable :: a(:)
    integer n,gcd1, largenum
  
    largenum=100 !To read numbers from source file
    n=0
    allocate (a(n))
    do i=1, largenum
        open (1,file='gcd.dat')
        read (1,*, end=10) a(i)
        n=n+1
    end do
  
    10 write (*,20) "Finding the GCD of ",n," numbers" !To display the input
    20 format (A,I3,A)
    write (*,*) "The numbers are"
    write(*,*)
    do i=1,n
          write (*,*) a(i)
    end do
  
    gcd1=a(1)!To find the GCD
    do i=2,n
        gcd1=gcd(gcd1,a(i))
    end do
    write(*,*)
    write(*,*) "The GCD is ",gcd1
    
    contains !To create the GCD function to be used in the previous section
    integer function gcd(x,y)
        integer x,y

        y1=max(x,y)
         x1=min(x,y)
 
        do
              if (mod(y1,x1)==0) then
                gcd=x1
                return
                exit
                else
                 temp=x1 !Assigning x1 and y1 values without using a temp variable gives wrong results
                 x1=mod(y1,x1)
                 y1=temp
             end if
            end do

    end function gcd
  
end program gcd_all

Sample Output